글 | 강성훈
1. 전압 분배 회로
2. 저역 통과 필터
3. 고역 통과 필터
4. 고차 필터
5. 대역 통과 필터
6. 대역 차단 필터
7. 스피커 네트워크의 크로스오버 주파수에서 위상 결합
8. 이퀄라이저의 위상 변이
- 필터는 특정 주파수 이상이나 이하의 주파수를 차단하는 회로이다. 필터를 이용하여 불필요한 신호를 커트하여 음질을 보정한다. 그리고 스피커 네트워크 필터, 이퀄라이저를 만드는데도 활용되고 있다.
- 필터는 음향 기술에서 없어서는 안되는 중요한 회로이다. 그러나 필터를 통과하면 주파수 특성이 변하고, 위상 변이도 생기므로 특성을 잘 이해하고 사용해야 한다.
4. 고차 필터
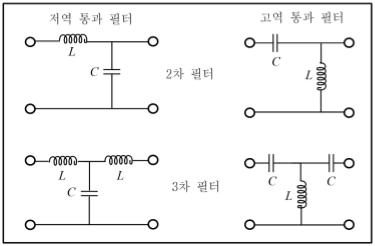
하나의 인덕터나 커패시터를 사용하여 만든 필터를 1차 필터(first-order filter)라고 한다. 그리고 그림 17과 같이 소자를 2개 사용하면 2차 필터, 3개 사용하면 3차 필터라고 한다.
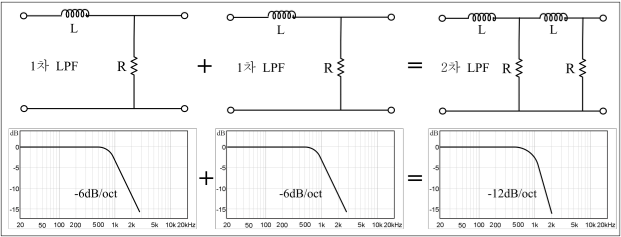
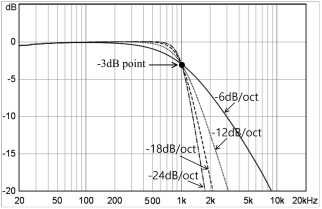
1차 필터의 감쇠 기울기는 주파수가 1 옥타브 증가할 때마다 이득이 -6dB씩 감쇠된다(-6dB/oct). 그림 18과 같이 1차 필터 2개를 캐스케이드(cascade)로 연결하면 2차 필터가 되고, 기울기는 -12dB/oct가 된다. 즉, 1차 필터 당 기울기는 -6dB/oct이고, 2차 필터는 -12dB/oct, 3차 필터는 -18dB/oct, 4차 필터는 -24dB/oct가 된다(그림 19). 이와 같이 1차 필터 당 기울기는 6dB씩 증가되고, 차수가 높을수록 기울기가 급격해진다.
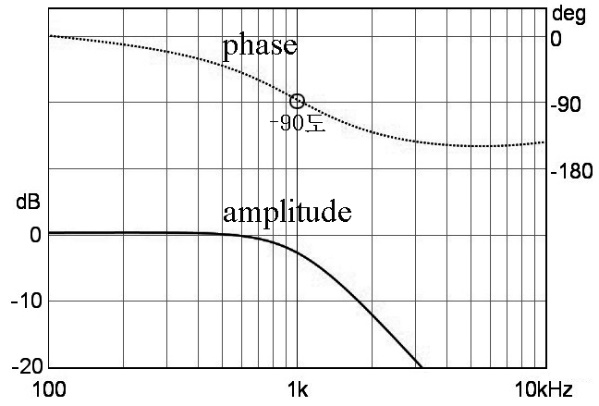
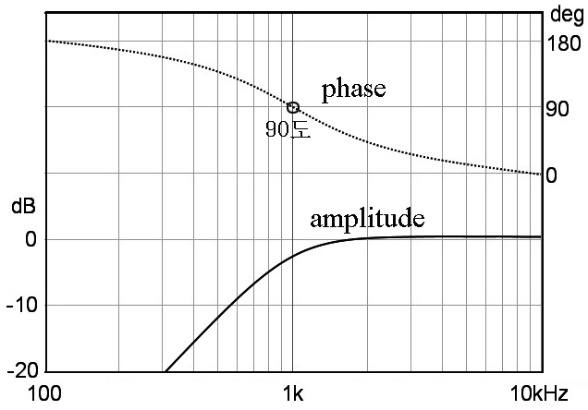
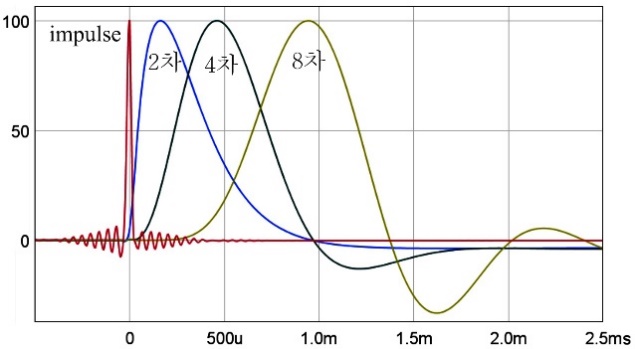
또, 신호가 필터를 통과하면 위상이 변이되고, 차단 주파수에서 1차 필터 당 45도씩 위상차가 생기고(그림 10, 그림 15 참조), 2차 필터는 그림 20과 같이 90도 위상 차가 생긴다. 그리고 3차 필터는 135도, 4차 필터는 180도 위상이 변이된다. 필터의 기울기가 급격할수록 불필요한 성분을 차단하는 성능은 좋지만, 위상도 급격하게 변이된다. 그리고 필터 차수가 높아지면 그림 21과 같이 출력 신호의 시간 지연이 길어진다.
5. 대역 통과 필터
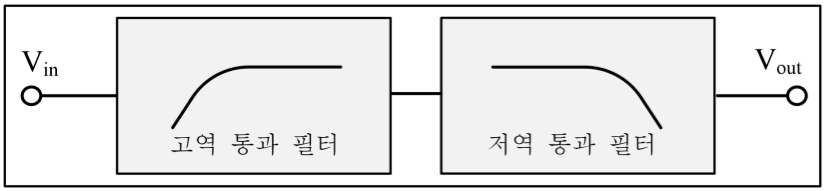
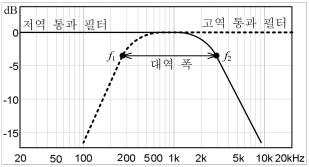
대역 통과 필터(band pass filter)는 특정 주파수 대역의 신호만 통과시키고, 통과 대역 이하와 이상의 주파수 신호는 차단하는 필터이다. 대역 통과 필터는 저역 통과 필터와 고역 통과 필터를 조합하여 구성한다(그림 22~23).
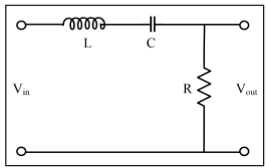
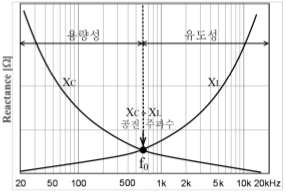
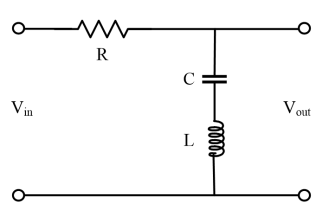
대역 통과 필터의 회로는 그림 24와 같다. R L C 직렬 회로에서 그림 25와 같이 주파수가 아주 낮은 영역에서는 XC 값은 크고, XL 값은 작다. 그리고 주파수가 증가하면 XC 값은 점차 감소하고 XL 값은 증가한다. 이 때 두 리액턴스 값이 같아지는 주파수, 즉 XL=XC의 주파수에서는 두 리액턴스가 상쇄되어 전체 리액턴스 값은 0Ω이 되므로 출력 전압은 최대가 된다. 이 상태를 직렬 공진이라고 한다. 대역 통과 필터의 중심 주파수(f0)는 (14) 식과 같다.
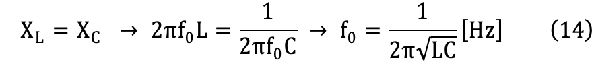
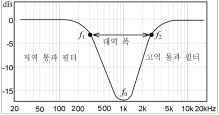
출력 전압은 그림 26과 같이 공진 주파수 f0에서 최대가 되는 대역 통과 필터 특성이 된다. 이 때 공진 주파수가 대역 통과 필터의 중심 주파수(center frequency) f0이다.
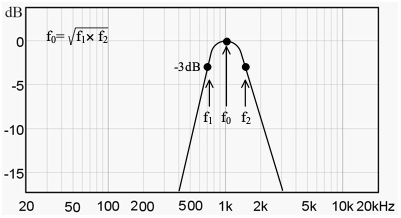
그림 26에서 f1, f2는 차단 주파수이고, 중심 주파수 f0와 f1, f2와의 사이에는 (15) 식과 같은 관계가 있다.
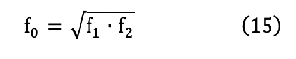
또, f1과 f2는 (16) 식과 같은 관계가 있다. 여기에서 n=1이면 1 옥타브 밴드 패스 필터, n=1/3이면 1/3 옥타브 밴드 패스 필터이다.
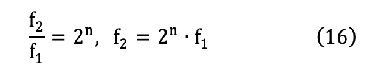
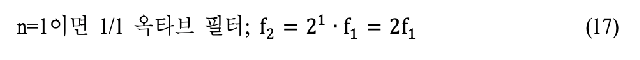
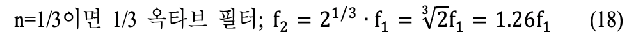
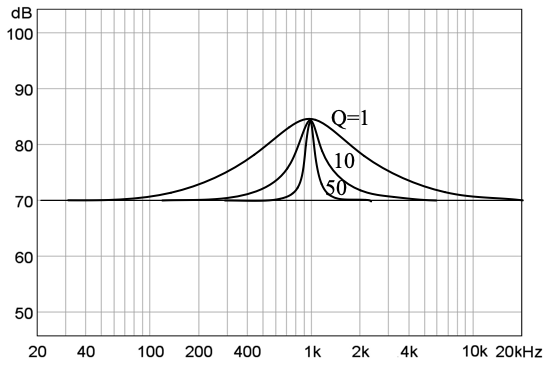
f2와 f1과의 차이를 대역 폭(bandwidth, BW)이라고 하며, (19) 식과 같다. 또, 대역 폭의 넓은 정도를 나타내는 (20) 식으로 정의되는 Q(quality factor)가 있다. 그림 27과 같이 Q 값이 클수록 대역 폭은 좁고, Q 값이 작을수록 대역 폭이 넓다.
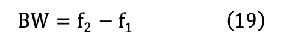
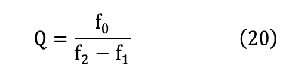
밴드 패스 필터는 주파수 분석에 이용되고, 1 옥타브 밴드 패스 필터(one octave band pass filter)와 1/3 옥타브 밴드 패스 필터(one-third octave band pass filter)가 있다. 그림 28에는 1 옥타브 밴드와 1/3 옥타브 밴드의 대역 폭을 비교하여 나타낸다.
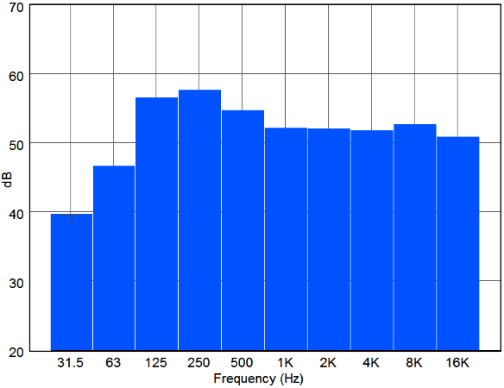
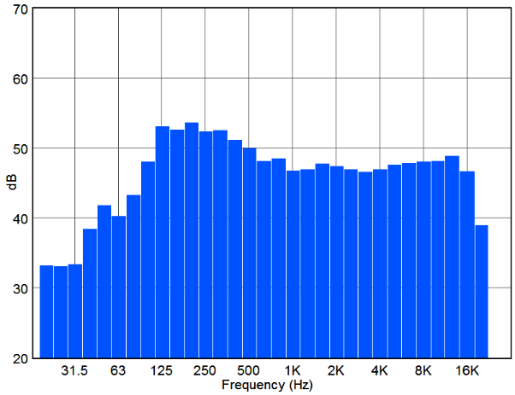
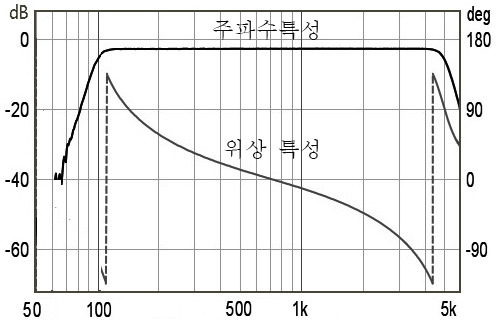
그림 29에는 100Hz~5kHz 대역 통과 필터를 건 진폭 특성과 위상 특성을 나타낸다. 저역은 고역 통과 필터를 거치고, 고역은 저역 통과 필터를 거치므로 저역에서 고역으로 갈수록 +에서 –로 위상이 변이된다.
6. 대역 차단 필터
대역 차단 필터(band stop filter)는 저역 통과 필터와 고역 통과 필터로 구성된다. 저역 통과 필터의 차단 주파수를 고역 통과 필터의 차단 주파수보다 낮게 하고, 고역 통과 필터의 차단 주파수를 저역 통과 필터의 차단 주파수보다 높게 하면 그림 30과 같이 대역 차단 필터가 된다.
대역 차단 필터 회로는 그림 31과 같다. 공진 주파수에서 리액턴스가 최소가 되므로 출력 전압은 최소가 된다.
7. 스피커 네트워크의 크로스오버 주파수에서 위상 결합
필터는 그림 32와 같이 복합형 스피커의 네트워크 필터로 사용된다. 2웨이 스피커에는 저역 통과 필터와 고역 통과 필터를 사용하고, 3웨이 스피커에는 저역 통과 필터, 대역 통과 필터, 고역 통과 필터를 사용한다. 필터를 정확하게 활용하기 위해서는 다음과 같은 특성을 이해해야 한다.
1차 저역 통과 필터는 차단 주파수에서 출력 신호는 입력 신호보다 45도 지연된다(13.33a). 그리고 2차 필터는 90도, 3차 필터는 135도 4차 필터는 180도 위상 지연된다. 1차 고역 통과 필터는 차단 주파수에서 출력 신호는 입력 신호보다 45도 앞선다(그림 33b). 그리고 2차 필터는 90도, 3차 필터는 135도 4차 필터는 180도 앞선다. 이 내용은 4절과 5절을 참조한다.
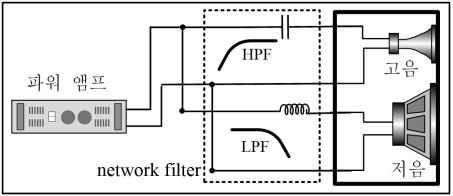
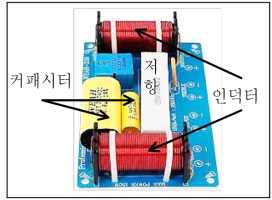
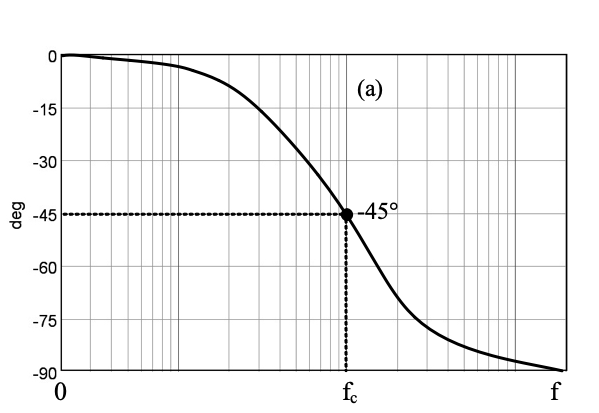
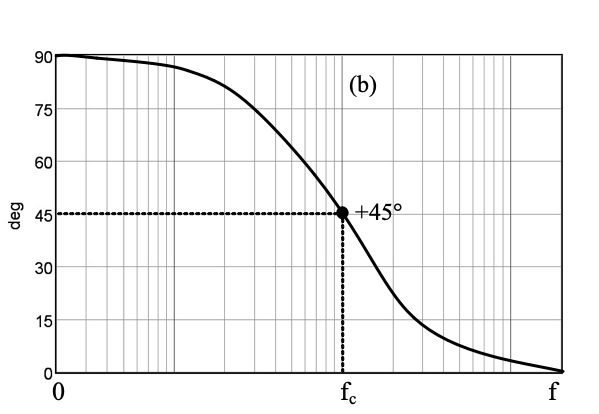
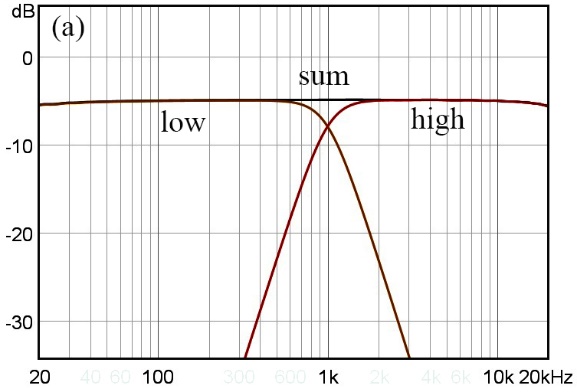
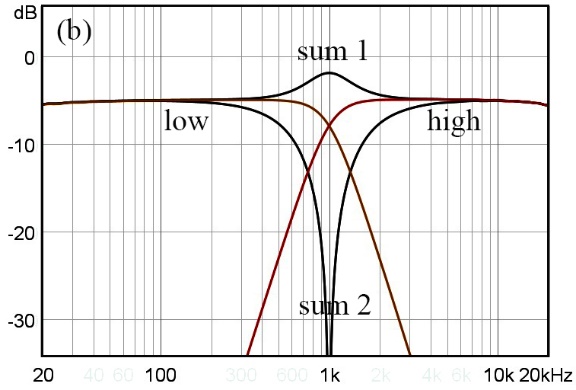
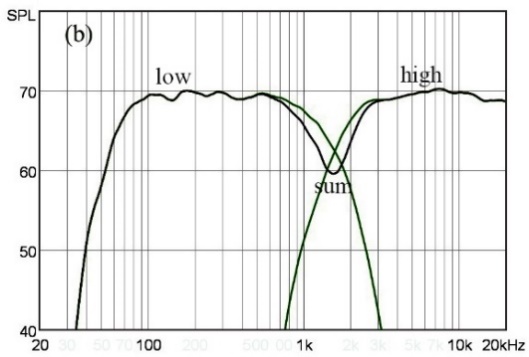
그림 34는 2웨이 스피커의 저역과 고역 통과 필터의 특성이 합성된 주파수 특성(sum)을 나타낸다. 그림 34(a)는 두 필터가 크로스오버 주파수에서 동 위상으로 결합된 특성이다. 그림 (b)는 두 필터 간의 위상 차가 있는 특성으로서 크로스오버 주파수에서 부스트 되거나(sum 1) 상쇄되는 특성을(sum 2) 나타낸다. 이와 같이 크로스오버 주파수에서 두 필터의 위상이 일치하면 주파수 특성이 평탄하고, 일치하지 않으면 피크나 딥이 생긴다.
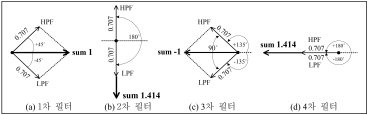
Butterworth 1차 HPF 출력 전압은 차단 주파수에서 0.707(-3dB)이고, 위상 변이는 +45도이다. LPF 출력 전압은 차단 주파수에서 0.707(-3dB)이고, 위상 변이는 -45도이다. 이것을 벡터도로 나타내면 그림 35(a)와 같이 LPF와 HPF 출력 신호의 위상 차는 90도가 되고, 두 신호 합은 1(=√0.7072+0.7072)이 되어 평탄한 특성이 된다.
2차 버터워스 HPF는 그림 35(b)와 같이 출력의 위상 변이는 +90도, LPF 위상 변이는 -90도이고, 출력 합은 180도 위상 차가 생기므로 크로스오버 주파수에서 음은 상쇄된다(그림 34b sum 2).
그리고 어느 한 쪽 필터를 역 위상으로 하면, 합은 1.414 (=0.707+0.707)가 되어 3dB 부스트 된다(그림 34b sum 1).
3차 필터는 크로스오버 주파수에서 HPF 위상은 +135도, LPF 위상은 -135도가 되고, 두 신호 간의 위상 차는 90도가 된다(그림 35c). 그 결과 합은 1이 되지만, 출력 신호는 입력 신호와 180도 위상 차가 나는 역 위상이 된다.
4차 버터워스 필터는 합이 1.414(= 0.707 + 0.707)가 되므로 3dB 피크가 생긴다. 그리고 출력은 입력과 180도 위상 차가 생긴다(그림 35d).
L-R 필터는 크로스오버 주파수에서 출력 전압은 0.5이다. 그림 36(a)는 L-R 2차 필터로서 각 벡터의 크기는 0.5이며, 위상 차는 180도가 된다.
따라서 이것을 더하면 크로스오버 주파수에서 두 신호는 상쇄되고, 두 필터 중에서 어느 한 쪽을 역 위상으로 접속하면 합은 1이 되어 주파수 특성이 평탄하다. 4차 L-R 필터는 합은 1이 되고(그림 36b), 8차 필터의 합도 1이 된다.
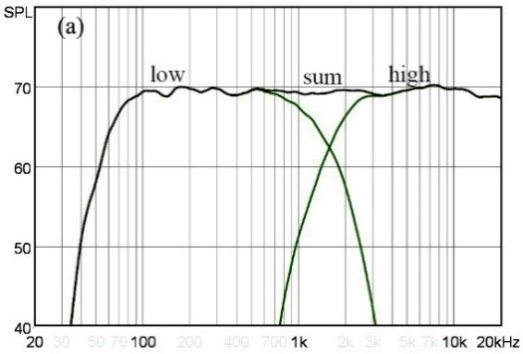
그림 37(a)는 두 필터가 크로스오버 주파수에서 동 위상으로 결합된 특성이다. 그림 (b)는 크로스오버 주파수에서 우퍼용 저역 통과 필터와 트위터용 고역 통과 필터 간의 위상이 180도 차이에 의해 크로스오버 주파수 대역이 상쇄되어 딥이 생긴 특성이다.
크로스오버 주파수에서 특성은 아주 중요하다. 크로스오버 주파수에서 두 유닛의 위상이 일치되지 않으면, 음이 상쇄되어 딥이 생기고 음질이 좋지 않다. 대부분의 크로스오버 주파수는 1~4kHz 대역에 존재하고, 이 대역은 명료성 대역이므로 위상이 정확하게 일치하지 않으면 음이 명료하지 않다.
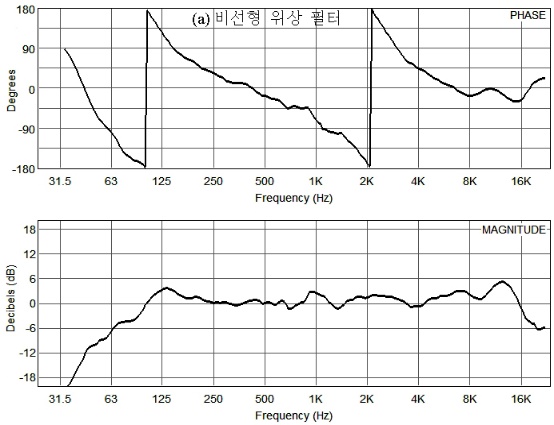
이상에서 설명한 버터워스 필터, L-R 필터와 같은 아날로그 필터는 차수가 변하면 위상 특성이 변이된다. 이러한 필터를 IIR(infinite impulse response) 필터라고 한다.
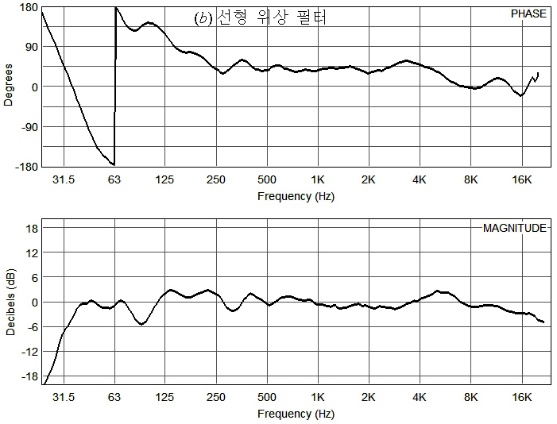
반면에 FIR(finite impulse response) 필터는 기울기가 바뀌어도 위상이 변하지 않은 선형 위상 필터이다. 그림 38(b)와 같이 선형 위상 필터는 위상이 회전하지 않고 평탄한 것이 특징이다.
8. 이퀄라이저의 위상 변이
필터는 음질을 보정하는 그래픽 이퀄라이저, 파라메트릭 이퀄라이저, 쉘빙 이퀄라이저, 노치 필터로 사용된다. 그래픽 이퀄라이저는 그림 45와 같이 대역 통과 필터와 대역 저지 필터로 구성된다.
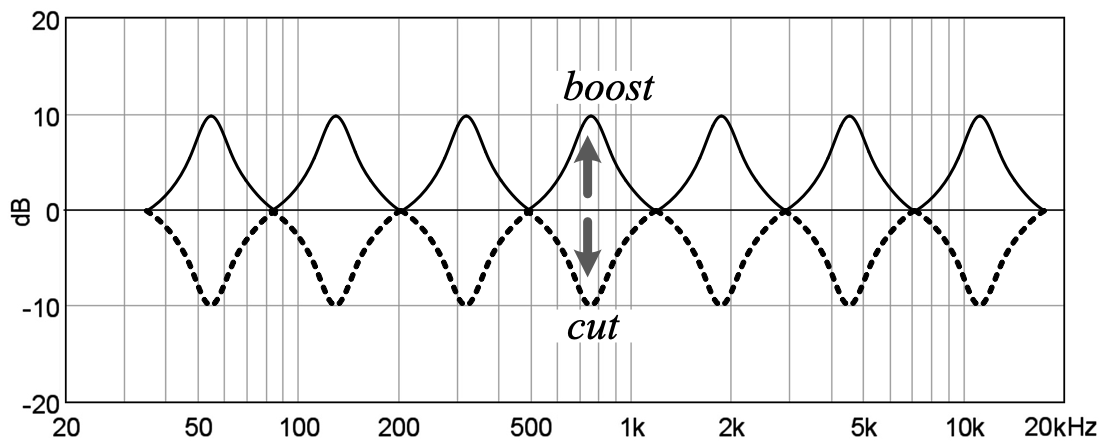
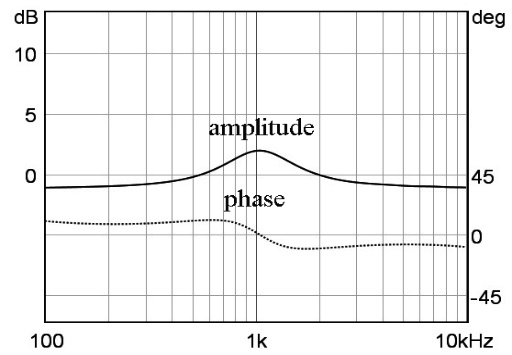
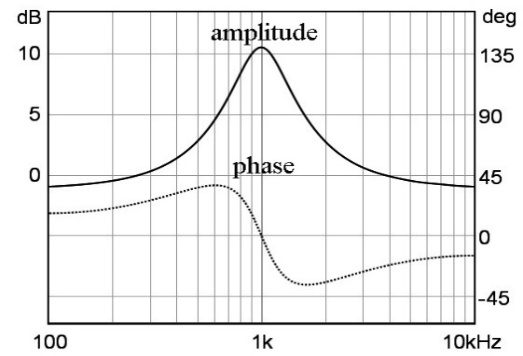
대역 통과 필터와 대역 차단 필터의 이득을 가변하면 위상 특성이 변이된다. 따라서 이퀄라이저의 슬라이더를 가변하면 그림 40과 같이 위상이 변이 되고, 슬라이더를 많이 부스트 하면 위상도 더 많이 변이된다. 그러나 이 위상 변이는 거의 지각되지 않는다.
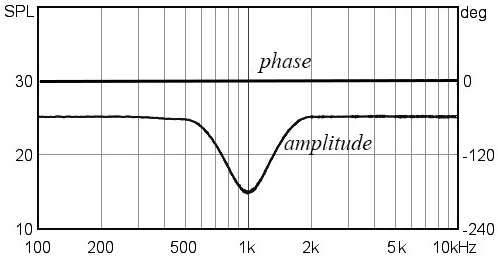
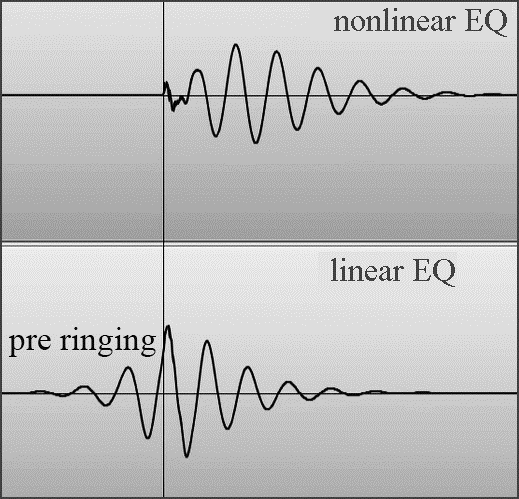
한편, 선형 위상 이퀄라이저는 그림 41과 같이 슬라이더를 가변해도 위상 특성이 변하지 않는다. 그러나 선형 위상 이퀄라이저는 슬라이더를 가변하면, pre ringing(또는 pre echo)이 발생되는 것도 있다. 이것은 일종의 디지털 이퀄라이저의 왜곡이며, 어택 음이 빠른 음은 둔탁하고 힘이 없는 음으로 들린다.
